PEFT 预训练语言模型的高效参数微调方法

预训练语言模型在发展过程中催生出各种调参方法和小的机制；反过来，这些方法和机制也为语言模型的下一次飞跃积蓄力量。

背景

基于 Transformer 的预训练语言模型在广泛的 NLP 任务取得良好表现，预训练 + 微调也逐渐成为 NLP 领域的主流范式。但是随着模型参数量的与日俱增，传统全微调方式表现出诸多问题：

• 需更新全部预训练参数，耗时且计算成本高；
• 各下游任务不共享参数，独立存储和部署；
• 微调数据集远小于预训练数据集，容易导致过拟合。

为解决上述问题，高效参数微调（Parameter-Efficient Fine-Tuning, PEFT）被提出来，使得微调 PLM 在实际应用中切实可行。PEFT 的思想是：设计一种通用的微调方法，它在性能上能够媲美传统全微调方式，但在面向下游任务训练时仅学习少量的新增参数或部分预训练参数。

PEFT 方法主要有三条独立发展的分支：局部微调，增式微调，再参数化微调。

预训练语言模型

Transformer

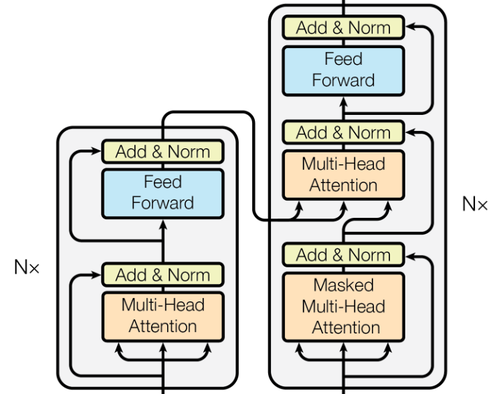
当前绝大多数 PLM 都以 Vanilla 等人 的 Transformer 为基础架构。Transformer 是 seq2seq 模型，由编码器和解码器构成。其中，编码器和解码器同为 L 层的栈。编码器的每层都由前后连接的一个多头自注意力模块和一个前馈网络模块（FFN）组成。解码器的每层则在此基础上在多头自注意力模块和 FFN 当中额外插入了一个交叉注意力模块。同时，为了构建更深的网络，每个模块的输出都使用了 残差连接，并进行 层归一化。最后，对解码器的自注意力模块做掩码，防止当前位置的输出能注意到其后续位置的输入。

Transformer

全微调

全微调 是指，在面向特定的下游任务和数据训练 PLM 时，学习整个模型的全部层和全部参数。在全微调过程中，模型所有的参数将通过反向传播和梯度下降等技术更新，以最小化特定于任务的损失函数。预训练参数为参数优化提供了较好的初始点，使得梯度下降不容易落入局部最优。

高效参数微调方法

局部微调

局部微调（Partial fine-tuning），旨在通过选择对下游任务至关重要的预训练参数而丢弃不重要的参数来减少需要学习的参数量，期间不引入额外的新的参数。

偏置更新

Bitfit（Bias-terms Fine-tuning） 通过仅更新偏置项和特定于任务的分类层，并保持 PLM 中的大多数参数冻结来实现高效调参。偏置项参数涉及到多头注意力层中 $$、$$、$$ 的计算，注意力头的组合，以及 FFN 层和归一化层中的计算。

$$

$$

$$

U/S-BitFit 在 Bitfit 基础上结合了 NAS 算法 和剪枝技术，来自动确定需要对网络的哪些参数进行微调。U-BitFit（Unstructed Bitfit）根据对 PEFT 参数 W 进行剪枝所导致的训练损失变化的一阶近似，即 $$，来决定要对哪些 PEFT 参数进行剪枝。而 S-BitFit（Structured Bitfit）则对总体偏差更新 $$ 的损失求和。

权重掩蔽

权重掩蔽采用阈值、Fisher 信息等剪枝准则衡量预训练权重的重要性，构造 0-1 掩码矩阵进行权值掩码。具体来说，对于权重矩阵 $$ ，它构造与 $$ 具有相同大小的 0-1 掩码矩阵 $$ 。0 表示当前忽略当前位置的权重，1 表示在训练中保留并更新该权重。

Threshold-Mask 利用阈值构造 0-1 掩码矩阵，通过逐元素乘法筛选注意力层和FFN 层的预训练权重 $$ ，表示为 $$（$$ 表示 Hadamard 乘积）。首先，随机生成均匀分布的实数矩阵 $$，$$ 具有和 $$，$$ 相同的大小。之后，如果 $$ 的某个元素超过了给定阈值 $$ ，则 $$ 对应位置的元素设置为 1，否则设置为 0，即 $$。在之后的训练过程中，通过如下公式来更新 $$ 从而更新 $$ ，其中 $$ 是步长：

$$

FISH-Mask（Fisher-Induced Sparse uncHanging）使用权重的 Fisher 信息来衡量其重要性并构造稀疏 0-1 矩阵 $$ 。FISH-Mask 选择具有最大 Fisher 信息的 top-$$ 参数，将 $$ 在这 $$ 个参数所在位置对应的元素设置为 1，其余位置设置为 0，即 $$。其中，$$ 是根据期望的矩阵稀疏程度预设的。

增式微调

增式微调（Additive fine-tuning），考虑为特定下游任务引入额外的可训练参数，其参数量远小于原始模型的参数，在训练时主要训练这一部分的参数而保持原预训练参数冻结不变。

Adapter

Adapter 的思想最开始被引入多领域图像分类中，用于在不同的图像领域之间高效地迁移知识，主要实现了不同领域间高度的参数共享。

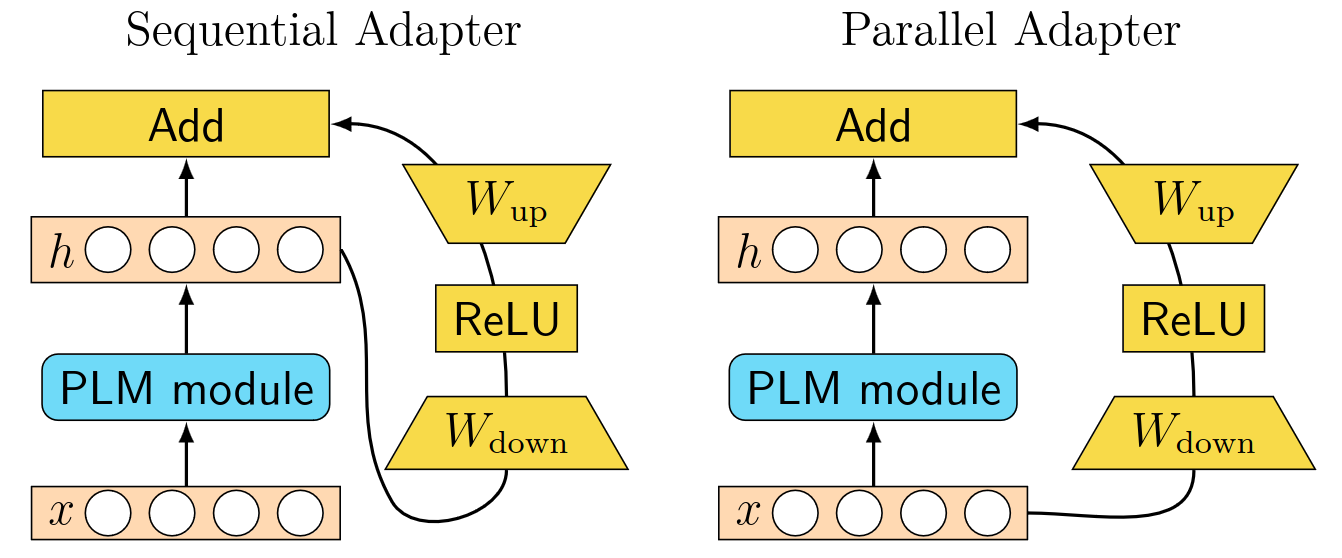
Sequential Adapter 通过给 Transformer 添加 Adapter 模块将其引入 NLP 领域。在针对下游任务训练时，除了引入的 Adapter 模块的参数，其余参数均保持预训练后的状态。具体来说，全部 Adapter 模块被顺序地插入在注意力层和 FFN 层之后，残差连接和层归一化之前。每个 Adapter 模块都由向下投影，非线性激活函数和向上投影三部分组成，并将向下投影的输入和向上投影的输出做残差连接。对于输入 $$，带 ReLU 激活函数的 Adapter 的输出可以表示为如下公式。在微调期间只有 $$ 和 $$ 需要更新。

$$

受 Sequential Adapter 启发，后续出现了许多基于 Adapter 的 PEFT 方法。Residual Adapter 通过仅在 FFN 层和归一化层之后插入 Adapter 模块来进一步提高调参效率。Parallel Adapter 与 Sequential Adapter 顺序地插入 Adapter 模块不同。如图，它将 Adapter 模块与注意力层和 FFN 层并联，两者共享相同的输入，并将各自输出的和作为最终的输出。AdapterDrop 删除 Transformer 每层中对给定任务不重要的适配器，进一步提高推理效率。

Adapter 对比

软提示

软提示微调（soft prompt fine-tuning）是这样一类微调方法，将可学习的连续向量插入模型的嵌入层输出或隐藏层状态，这些插入的连续向量称为软提示（soft prompt）。与手动设计的硬提示（hard prompt）不同，软提示是根据任务特定的训练数据，在离散标记空间中搜索生成的。由于提示内容可以根据具体的任务和训练数据进行优化和调整，软提示在微调过程中表现出更多的灵活性和适应性。

Prompt-tuning 引入额外的 $$ 个可学习的提示标记，$$，将其与模型输入 $$ 拼接得到模型的最终输入 $$。

$$

在微调期间，梯度下降仅更新来自 $$ 的提示参数，而保持其他的预训练参数冻结。这样，Prompt-tuning 的参数成本取决于提示长度 $$ 和标记词的嵌入向量的维度 d 的乘积。实验证明，扩充提示的句子长度而不是仅仅使用一个标记对于提高模型性能至关重要。

Prefix-tuning 提出将软提示 $$ 附加到多头注意力层中的隐藏层状态，而不是像 Prompt-tuning 那样将提示附加到模型的输入。它将两组前缀向量 $$ 和 $$ 分别与注意力层中的 $$ 和 $$ 拼接，之后再进入注意力机制。同时，考虑到直接优化软提示可能导致不稳定，引入一个 FFN，在进行拼接操作前先参数化 $$ 和 $$ 得到实际与 $$、$$ 拼接的向量 $$ 和 $$。带有 Prefix-tuning 的注意力机制可以表示为如下公式。

$$

在训练期间，只有 $$，$$ 和 FFN 的参数会被优化，而其他 PLMs 的参数都保持冻结状态。训练结束后，将FFN 舍弃，仅保留更新后的 $$ 和 $$ 用于推断。

P-tuning 同样考虑将软提示 $$ 插入模型输入。不同的是，P-tuning 将这些提示拼接起来形成一个模板，并将其映射为 $$ 的形式，其中 $$ 是预训练的嵌入层。P-tuning 的训练目标是优化这些连续提示 $$。因为 PLM 的权重被固定且仅有少量参数需要微调，提示模板可以在少样本情景下高效学习。P-tuning 利用一个双向长短期记忆网络（Bi-LSTM）和一个由 ReLU 激活的多层感知机来初始化软提示的嵌入向量：$$。

其他方法

LST（Ladder Side-Tuning）训练一个额外的阶梯边缘网络（ladder side network）而不是直接在原骨干网络上训练。骨干网络与边缘网络之间通过名为阶梯的捷径连接，用以将骨干网络的中间激活值传递给边缘网络作为其输入。在训练过程中，反向传播通过边缘网络和阶梯捷径进行，而不经过骨干网络的神经元连接，从而减少了微调参数的数量。此外，LST 还利用 结构性剪枝 来检索一个较小的剪枝网络来初始化边缘网络，并删除边缘网络的某些层，进一步提高调参效率。

AttentionFusion 引入了后期融合技术，通过组合来自不同任务或层的特征及表示来生成最终的联合表示，以调整每个 token 表示的重要性。对于给定的任务 $$，假设与之对应 的注意力查询向量为 $$，第 $$ 层的第 $$ 个 token 的向量表示为 $$。那么，任务 $$ 的第 $$ 个 token 的最终表示 $$ 可以表示为：

$$

其中，$$ 表示任务 $$ 的第 $$ 层的第 $$ 个 token 的注意力权重。在 AttentionFusion 中需要更新的额外参数的数量由查询向量 $$ 的大小决定，$$ 的尺寸与预训练编码器的隐藏维度相同。通过使用注意力权重作为额外的可训练参数，AttentionFusion 动态地调整每个 token 表示的重要性。

再参数化微调

再参数化微调（Reparameterized fine-tuning），是指在允许对高维矩阵进行操作的同时，利用低秩变换减少可训练参数的数量。

低秩分解

研究发现，语言模型虽然参数众多，但是起到关键作用的还是其中低秩的本质维度。低秩分解试图找到一个较低秩的矩阵，该矩阵捕获原始矩阵的基本信息，但计算量要比原始矩阵小。对于模型参数 $$ 和训练时所产生的更新 $$ ，通过将 $$ 再参数化为一个低秩矩阵来降低计算复杂度和减少内存使用。再参数化包括低秩升降维投影和 Kronecker 乘积投影等方法。

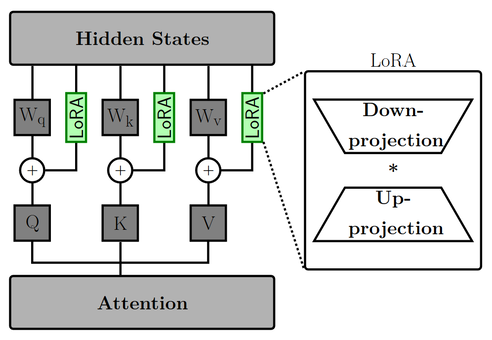
LoRA（Low-Rank Adaption）为权重更新引入两个可学习的低秩矩阵，分别是降维投影矩阵（down-projection）和升维投影矩阵（up-projection）。在注意力层当中，降维投影矩阵和升维投影矩阵与 $$、$$、$$ 矩阵并联来生成 $$、$$、$$。

$$

LoRA

对于预训练的权重矩阵 $$, LoRA 将权重的更新量 $$ 低秩分解 $$。训练时，冻结 PLM 的权重，仅更新 LoRA 部分的低秩矩阵，也就是 $$ 和 $$（$$）。

这样，LoRA 实际上学习的是针对训练的特定任务，在原始权重的基础上应该更新的更新量 $$ 。在推理阶段，原本预训练语言模型的参数被替换为 LoRA 部分的权重与原始权重的和。因此，训练得到的模型参数量与原始模型完全相同，不会增加额外的计算资源。

KronA（Kronecker Adapter）在结构上和 LoRA 类似，不同之处在与 KronA 将 LoRA 使用的低秩分解替换为 Kronecker 乘积 分解，$$。Kronecker 乘积分解维持了输入矩阵的秩（$$），确保重要信息不会被遗漏。此外 Kronecker 乘积通过避免对 Kronecker 乘积矩阵的显式重构，减少了所需的浮点运算次数，从而加快了计算速度。KronA 有两个变体：$$ 和 $$。前者将 KronA 模块与 FFN 层并联，后者将 KronA 模块插入在 FFN 层后，并执行一个可学习的残差连接。

LoRA 衍生

LoRA 的衍生品是指在 LoRA 基础上改进的一系列 PEFT 方法，包括低秩调整、LoRA 引导的预训练权重更新、量化调整、基于 LoRA 的改进、基于 LoRA 的多任务微调。这里主要介绍低秩调整的三种代表方法。

DyLoRA（Dynamic LoRA）主要克服了 LoRA 的两点限制：1）LoRA 部分的秩是固定的，在训练前后不会发生变化；2）确定 LoRA 最佳的秩数需要穷举搜索和大量的工作。DyLoRA 在一个秩数范围，而不是单个秩数下训练 LoRA，从而允许秩数动态调整。

在训练阶段，DyLoRA 迭代秩数范围 $$，每次迭代随机地从中取出一个秩数 $$。之后，用这个随机选取的秩数对升降维矩阵进行裁剪：$$。每次迭代中的参数更新量可以表示为 $$。通过动态的和无需搜索的低秩调整，DyLoRA 减少了为特定任务搜寻最优秩数的计算成本和时间开销。

AdaLoRA（Adaptive Low-Rank Adaptation）对参数更新量 $$ 进行奇异值分解（SVD，Singular Value Decomposition），分解为 $$。其中，$$ 和 $$ 都是正交矩阵，$$ 是对角元素为 $$ 的对角矩阵，$$ 是矩阵 $$ 的秩数。在训练阶段，$$ 和 $$ 按带有正则的高斯分布初始化，以确保其正交性，而 $$ 则被初始化为全 0 矩阵。$$ 秩的确定在迭代中完成。AdaLoRA 使用基于敏感度的重要性评分改进的新方法修剪不重要的奇异值以调整 $$。

IncreLoRA 根据训练过程中分配给每个模块的重要性分数，来改变可训练参数的秩数，从而动态地将可训练参数纳入 LoRA 模块中。在分配过程中，较不重要的模块被分配给较低的秩数，较重要的模块被分配给较高的秩数。分配的秩数最低为 0，表示没有参数更新。IncreLoRA 中的参数更新可以表示为 $$，其中 $$ 是对角矩阵。$$ 可以是任意常数，$$ 是每个 LoRA 模块的秩。IncreLoRA 为每个模块设置了秩的上界，以控制参数的增长。此外，IncreLoRA 还引入了称为 advanced learning 特别预训练技术，确保每个新添加的参数具有较好的初始状态。通过这种方式，它防止了后续添加的参数训练不足，从而能更有效地利用增量参数的分配。最后，不同于 LoRA 仅对注意力层的查询（Q）、键（K）和值（V）的投影模块操作，IncreLoRA 将参数更新应用于模型中的所有的线性层。

总结

本文对 PLM 的 PEFT 方法进行了较为全面和结构化的整理，主要关注点在各种高效参数微调方法的实现思想方面。通过对 NLP 中的 PEFT 方法进行分类和比较，可以发现它们在思想上具有某种相通之处。除开增式微调方法，局部微调和再参数化微调都试图从海量的预训练参数中找寻对下游任务最重要的参数，舍弃较不重要的参数，因此基于各种各样的评估方法来对模型的各个模块进行估分和裁剪。而增式微调则通过引入额外的机制，试图将原预训练语言模型提供的高质量表示特征隐式地加以利用，在此期间诞生了许多优秀的调参方法如 Prompt-tuning、Prefix-tuning 和 P-tuning 等也在其他方面具有广泛的应用场景。预训练语言模型在发展过程中催生出各种调参方法和小的机制；反过来，这些方法和机制也为语言模型的下一次飞跃积蓄力量。